深入理解 Golang 中 container/heap
in Note with 0 comment
Golang heap 堆
深入理解 Golang 中 container/heap
in Note with 0 comment

Golang heap 堆

堆（Heap）

堆（Heap）是计算机科学中的一种特别的完全二叉树，可以在 O(log n) 时间复杂度内完成插入、删除和获取最值等操作。

若是满足以下特性，即可称为堆：“给定堆中任意节点P和C，若P是C的母节点，那么P的值会小于等于（或大于等于）C的值”。

若母节点的值恒小于等于子节点的值，此堆称为最小堆（min heap）；反之，若母节点的值恒大于等于子节点的值，此堆称为最大堆（max heap）。在堆中最顶端的那一个节点，称作根节点（root node），根节点本身没有母节点（parent node）。

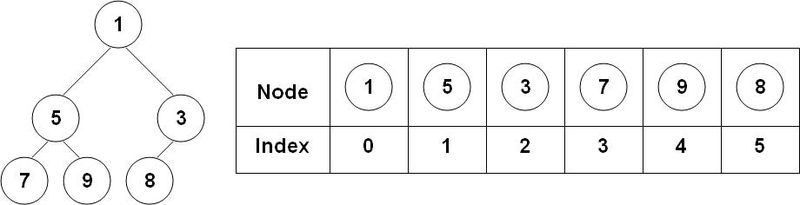
在 Go 中实现的 heap 是一个最小堆，即每个节点的值总是以该节点为根节点的子树的最小值。同时应当注意到，对于任意一个节点，假设其下表为i，则其父节点下标为(i - 1) / 2，其左子节点下标为2 * i + 1，其右子节点下标为2 * i + 2。

2020-01-10T07:25:02.png

下面是 container/heap 中每个操作的时间复杂度：

源码阅读

interface

在heap包中，定义了一个heap.Interface接口，只要实现该接口的数据结构，都可以作为一个堆来使用。

type Interface interface {
    sort.Interface
    Push(x interface{}) // add x as element Len()
    Pop() interface{}   // remove and return element Len() - 1.
}

其中继承了`sort.Interface，包含了Less/Len/Swap三个方法.

down 和 up

heap操作中最重要的两个方法是down和up。

down让一个节点下沉：

func down(h Interface, i0, n int) bool {
    i := i0
    for {
        // j1为左子节点下标
        j1 := 2*i + 1
        if j1 >= n || j1 < 0 { // j1 < 0 after int overflow
            break
        }
        j := j1 // left child
        // j2为右子节点下标，j为最小的子节点的下标
        if j2 := j1 + 1; j2 < n && !h.Less(j1, j2) {
            j = j2 // = 2*i + 2  // right child
        }
        // 如果最小的子节点不小于父节点，则已经满足最小堆条件，退出
        if !h.Less(j, i) {
            break
        }
        // 如果最小的子节点小于父节点，则交换这两个节点
        h.Swap(i, j)
        // 让父节点继续下沉
        i = j
    }
    return i > i0
}

up让一个节点上升：

func up(h Interface, j int) {
    for {
        // i为父节点下标
        i := (j - 1) / 2 // parent
        // 如果该节点不小于父节点，则满足最小堆条件，退出
        if i == j || !h.Less(j, i) {
            break
        }
        // 如果该节点小于父节点，则交换这两个节点
        h.Swap(i, j)
        // 让该节点继续上升
        j = i
    }
}

Init

用于初始化堆

func Init(h Interface) {
    n := h.Len()
    // 最后一个节点下表为n-1，因此其父节点为(n-1-1)/2，即n/2-1
    for i := n/2 - 1; i >= 0; i-- {
        down(h, i, n)
    }
}

Push

Push的时候，先把新元素放置在结尾，然后让其上升。

func Push(h Interface, x interface{}) {
    h.Push(x)
    up(h, h.Len()-1)
}

Pop

Pop的时候，先把根节点和最后一个节点交换位置，然后让新的根节点下降。注意这里down的第三个参数是n的值为h.Len() - 1，因此新的根节点下降的过程中，原先的根节点位于最后的位置，不受影响。

func Pop(h Interface) interface{} {
    n := h.Len() - 1
    h.Swap(0, n)
    down(h, 0, n)
    return h.Pop()
}

Remove

Remove操作与Pop非常类似，先将需要移除的节点和最后一个节点交换位置，然后同时进行down和up操作。

func Remove(h Interface, i int) interface{} {
    n := h.Len() - 1
    if n != i {
        h.Swap(i, n)
        down(h, i, n)
        up(h, i)
    }
    return h.Pop()
}

Fix

当某个节点的值改变后，通过Fix操作来调整堆的结构。该操作实际上也是同时进行了down和up操作。
与先移除旧节点再添加新节点相比，Fix操作的复杂度要低一些。

func Fix(h Interface, i int) {
    if !down(h, i, h.Len()) {
        up(h, i)
    }
}

使用 heap 包

IntHeap 例子

官方例子：基于整型 int 实现一个最小堆。
下面是使用 []int 的 slice 结构来实现一个 heap，注意调用方式采用 heap 包的方法进行调用。

import (
    "container/heap"
    "fmt"
)

type IntHeap []int

func (h IntHeap) Len() int           { return len(h) }
func (h IntHeap) Less(i, j int) bool { return h[i] < h[j] }
func (h IntHeap) Swap(i, j int)      { h[i], h[j] = h[j], h[i] }

func (h *IntHeap) Pop() interface{} {
    old := *h
    n := len(old)
    // 将顶小堆元素与最后一个元素交换位置，在进行堆排序的结果
    x := old[n-1]
    *h = old[0 : n-1]
    return x
}

// 实现 Push 方法，插入新元素
func (h *IntHeap) Push(x interface{}) {
    *h = append(*h, x.(int))
}


func main() {
    h := &IntHeap{2, 1, 5, 13,11, 4, 3, 7, 9, 8, 0}
    heap.Init(h)                                // 将数组切片进行堆化
    fmt.Println(*h)
    fmt.Println(heap.Pop(h))                    // 调用 pop 0 返回移除的顶部最小元素
    heap.Push(h, 6)                             // 添加一个元素进入堆中进行堆化
    for len(*h) > 0 {
      fmt.Printf("%d \n", heap.Pop(h))
    }
}

优先队列例子

import (
    "container/heap"
    "fmt"
)

type Item struct {
    value    string // 优先级队列中的数据，可以是任意类型，这里使用string
    priority int    // 优先级队列中节点的优先级
    index    int    // index是该节点在堆中的位置
}

// 优先级队列需要实现heap的interface
type PriorityQueue []*Item

// 绑定Len方法
func (pq PriorityQueue) Len() int {
    return len(pq)
}

// 绑定Less方法，这里用的是小于号，生成的是小根堆
func (pq PriorityQueue) Less(i, j int) bool {
    return pq[i].priority < pq[j].priority
}

// 绑定swap方法
func (pq PriorityQueue) Swap(i, j int) {
    pq[i], pq[j] = pq[j], pq[i]
    pq[i].index, pq[j].index = i, j
}

// 绑定put方法，将index置为-1是为了标识该数据已经出了优先级队列了
func (pq *PriorityQueue) Pop() interface{} {
    old := *pq
    n := len(old)
    item := old[n-1]
    *pq = old[0 : n-1]
    item.index = -1
    return item
}

// 绑定push方法
func (pq *PriorityQueue) Push(x interface{}) {
    n := len(*pq)
    item := x.(*Item)
    item.index = n
    *pq = append(*pq, item)
}

// 更新修改了优先级和值的item在优先级队列中的位置
func (pq *PriorityQueue) update(item *Item, value string, priority int) {
    item.value = value
    item.priority = priority
    heap.Fix(pq, item.index)
}

func main() {
    // 创建节点并设计他们的优先级
    items := map[string]int{"二毛": 5, "张三": 3, "狗蛋": 9}
    i := 0
    pq := make(PriorityQueue, len(items)) // 创建优先级队列，并初始化
    for k, v := range items {             // 将节点放到优先级队列中
        pq[i] = &Item{
            value:    k,
            priority: v,
            index:    i}
        i++
    }
    heap.Init(&pq) // 初始化堆
    item := &Item{ // 创建一个item
        value:    "李四",
        priority: 1,
    }
    heap.Push(&pq, item)           // 入优先级队列
    pq.update(item, item.value, 6) // 更新item的优先级
    for len(pq) > 0 {
        item := heap.Pop(&pq).(*Item)
        fmt.Printf("%.2d:%s index:%.2d\n", item.priority, item.value, item.index)
    }
}
输出结果：
03:张三 index:-01
05:二毛 index:-01
06:李四 index:-01
09:狗蛋 index:-01

应用场景

参考

本文由 Chakhsu Lau 创作，采用 知识共享署名4.0 国际许可协议进行许可。
本站文章除注明转载/出处外，均为本站原创或翻译，转载前请务必署名。

← → ↓ ↑
Responses